reverse charm
There is a lot of talk about the "charm of opposites", and not only in mathematics. Remember that opposite numbers are those that differ only in sign: plus 7 and minus 7. The sum of opposite numbers is zero. But for us (i.e. mathematicians) the reciprocals are more interesting. If the product of numbers is equal to 1, then these numbers are inverse to each other. Every number has its opposite, every non-zero number has its inverse. The reciprocal of the reciprocal is the seed.
An inversion occurs wherever two quantities are related to each other so that if one increases, the other decreases at a corresponding rate. "Relevant" means that the product of these quantities does not change. We remember from school: this is an inverse proportion. If I want to get to my destination twice as fast (i.e. cut the time in half), I need to double my speed. If the volume of a sealed vessel with gas is reduced by n times, then its pressure will increase by n times.
In elementary education, we carefully distinguish between differential and relative comparisons. "How much more"? – “How many times more?”
Here are some school activities:
Task 1. Of the two positive values, the first is 5 times greater than the second and at the same time 5 times greater than the first. What are the dimensions?
Task 2. If one number is 3 greater than the second, and the second is 2 greater than the third, how much greater is the first number than the third? If the first positive number is twice the second, and the first number is three times the third, how many times is the first number greater than the third?
Task 3. In task 2, only natural numbers are allowed. Is such an arrangement as described there possible?
Task 4. Of the two positive values, the first is 5 times the second, and the second is 5 times the first. Is it possible?
The concept of "average" or "average" seems very simple. If I cycled 55 km on Monday, 45 km on Tuesday, and 80 km on Wednesday, on average I cycled 60 km per day. We wholeheartedly agree with these calculations, although they are a little strange because I have not driven 60 km in one day. We just as easily accept the shares of a person: if two hundred people visit a restaurant within six days, then the average daily rate is 33 and a third people. HM!
There are problems only with the average size. I like cycling. So I took advantage of the offer of the travel agency "Let's go with us" - they deliver luggage to the hotel, where the client rides a bicycle for recreational purposes. On Friday I drove for four hours: the first two at a speed of 24 km per hour. Then I got so tired that for the next two at a rate of only 16 per hour. What was my average speed? Of course (24+16)/2=20km=20km/h.
On Saturday, however, the luggage was left at the hotel, and I went to see the ruins of the castle, which is 24 km away, and having seen them, I returned. I drove an hour in one direction, returned back more slowly, at a speed of 16 km per hour. What was my average speed on the hotel-castle-hotel route? 20 km per hour? Of course not. After all, I drove a total of 48 km and it took me an hour (“there”) and an hour and a half back. 48 km in two and a half hours, i.e. hour 48/2,5=192/10=19,2 km! In this situation, the average speed is not the arithmetic mean, but the harmonic of the given values:
and this two-story formula can be read as follows: the harmonic mean of positive numbers is the reciprocal of the arithmetic mean of their reciprocal. The reciprocal of the sum of the reciprocals appears in many choruses of school assignments: if one worker digs hours, the other - b hours, then, working together, they dig on time. water pool (one per hour, the other at b hours). If one resistor has R1 and the other has R2, then they have a parallel resistance.
If one computer can solve a problem in seconds, another computer in b seconds, then when they work together...
Stop! This is where the analogy ends, because everything depends on the speed of the network: the efficiency of the connections. Workers can also hinder or help each other. If one man can dig a well in eight hours, can eighty workers do it in 1/10 of an hour (or 6 minutes)? If six porters take the piano to the first floor in 6 minutes, how long will it take one of them to deliver the piano to the sixtieth floor? The absurdity of such problems makes us remember the limited applicability of all mathematics to problems "from life".
About a powerful seller
The scales are no longer used. Recall that a weight was placed on one bowl of such scales, and the goods being weighed were placed on the other, and when the weight was in equilibrium, then the goods weighed as much as the weight. Of course, both arms of the weight load must be the same length, otherwise the weighing will be incorrect.
Oh right. Imagine a salesperson who has a weight with unequal leverage. However, he wants to be honest with the customers and weighs the goods in two batches. First, he puts a weight on one pan, and on the other a corresponding amount of goods - so that the scales are in balance. Then he weighs the second "half" of the goods in reverse order, that is, he puts the weight on the second bowl, and the goods on the first. Since the hands are unequal, the "halves" are never equal. And the seller's conscience is clear, and buyers praise his honesty: "What I removed here, I then added."
However, let's take a closer look at the behavior of a seller who wants to be honest despite the precarious weight. Let the arms of the balance have lengths a and b. If one of the bowls is loaded with a kilogram weight and the other with x goods, then the scales are in equilibrium if ax = b the first time and bx = a the second time. So, the first part of the goods is equal to b / a kilogram, the second part is a / b. Good weight has a = b, so the buyer will receive 2 kg of goods. Let's see what happens when a ≠ b. Then a – b ≠ 0 and from the reduced multiplication formula we have
We came to an unexpected result: the seemingly fair method of "averaging" the measurement in this case works to the benefit of the buyer, who receives more goods.
Task 5. (Important, by no means in mathematics!). A mosquito weighs 2,5 milligrams, and an elephant five tons (this is quite correct data). Calculate the arithmetic mean, geometric mean, and harmonic mean of the mosquito and elephant masses (weights). Check the calculations and see if they make any sense besides arithmetic exercises. Let's look at other examples of mathematical calculations that don't make sense in "real life". Tip: We've already looked at one example in this article. Does this mean that an anonymous student whose opinion I found on the Internet was right: “Math fools people with numbers”?
Yes, I agree that in the grandeur of mathematics, you can “fool” people - every second shampoo advertisement says that it increases fluffiness by some percentage. Shall we look for other examples of useful everyday tools that can be used for criminal activity?
Grams!
The title of this passage is a verb (first person plural) not a noun (nominative plural of one thousandth of a kilogram). Harmony implies order and music. For the ancient Greeks, music was a branch of science - it must be admitted that if we say so, we transfer the current meaning of the word "science" to the time before our era. Pythagoras lived in the XNUMXth century BC. Not only did he not know a computer, mobile phone and email, but he also did not know who Robert Lewandowski, Mieszko I, Charlemagne and Cicero were. He did not know either Arabic or even Roman numerals (they came into use around the XNUMXth century BC), he did not know what the Punic Wars were ... But he knew music ...
He knew that on stringed instruments the coefficients of vibration were inversely proportional to the length of the vibrating parts of the strings. He knew, he knew, he just couldn't express it the way we do it today.
The frequencies of the two string vibrations that make up an octave are in a 1:2 ratio, that is, the frequency of the higher note is twice the frequency of the lower one. The correct vibration ratio for fifth is 2:3, fourth is 3:4, pure major third is 4:5, minor third is 5:6. These are pleasant consonant intervals. Then there are two neutral ones, with vibration ratios of 6:7 and 7:8, then dissonant ones - a big tone (8:9), a small tone (9:10). These fractions (ratios) are like the ratios of successive members of a sequence that mathematicians (for this very reason) call the harmonic series:
is a theoretically infinite sum. The ratio of oscillations of the octave can be written as 2:4 and put a fifth between them: 2:3:4, that is, we will divide the octave into a fifth and a fourth. This is called harmonic segment division in mathematics:
Rice. 1. For a musician: dividing the octave AB into the fifth AC.For Mathematician: Harmonic Segmentation
What do I mean when I speak (above) of a theoretically infinite sum, such as the harmonic series? It turns out that such a sum can be any large number, the main thing is that we add for a long time. There are fewer and fewer ingredients, but there are more and more of them. What prevails? Here we enter the realm of mathematical analysis. It turns out that the ingredients are depleted, but not very quickly. I will show that by taking enough ingredients, I can sum up:
arbitrarily large. Let's take "for example" n = 1024. Let's group the words as shown in the figure:
In each parenthesis, each word is greater than the previous one, except, of course, the last one, which is equal to itself. In the following brackets, we have 2, 4, 8, 16, 32, 64, 128 and 512 components; the value of the sum in each parenthesis is greater than ½. All this is more than 5½. More accurate calculations would show that this amount is approximately 7,50918. Not much, but always, and you can see that by taking n any big, I can outperform any number. This incredibly slow (for example, we top ten with ingredients alone), but infinite growth has always fascinated mathematicians.
Journey to infinity with the harmonic series
Here's a puzzle to some pretty serious math. We have an unlimited supply of rectangular blocks (what can I say, rectangular!) with dimensions, say, 4 × 2 × 1. Consider a system consisting of several (on fig. 2 - four) blocks, arranged so that the first is inclined by ½ of its length, the second from above by ¼ and so on, the third by one sixth. Well, maybe to make it really stable, let's tilt the first brick a little less. It doesn't matter for calculations.
Rice. 2. Determining the center of gravity
It is also easy to understand that since the figure composed of the first two blocks (counting from above) has a center of symmetry at point B, then B is the center of gravity. Let's define geometrically the center of gravity of the system, composed of the three upper blocks. A very simple argument suffices here. Let's mentally divide the three-block composition into two upper ones and a third lower one. This center must lie on the section connecting the centers of gravity of the two parts. At what point in this episode?
There are two ways to designate. In the first, we will use the observation that this center must lie in the middle of the three-block pyramid, i.e., on a straight line intersecting the second, middle block. In the second way, we understand that since the two top blocks have a total mass of twice that of a single block #3 (top), the center of gravity on this section must be twice as close to B as it is to the center S of the third block. Similarly, we find the next point: we connect the found center of the three blocks with the center S of the fourth block. The center of the whole system is at height 2 and at the point that divides the segment by 1 to 3 (that is, by ¾ of its length).
The calculations that we will carry out a little further lead to the result shown in Fig. fig. 3. Consecutive centers of gravity are removed from the right edge of the lower block by: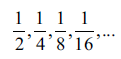
Thus, the projection of the center of gravity of the pyramid is always within the base. The tower will not topple over. Now let's look at fig. 3 and for a moment, let's use the fifth block from the top as the base (the one marked with the brighter color). Top inclined: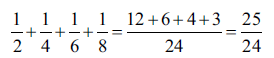
thus its left edge is 1 further than the right edge of the base. Here's the next swing:
What is the biggest swing? We already know! There is no greatest! Taking even the smallest blocks, you can get an overhang of one kilometer - unfortunately, only mathematically: the whole Earth would not be enough to build so many blocks!
Rice. 3. Add more blocks
Now the calculations that we left above. We will calculate all distances "horizontally" on the x-axis, because that's all there is to it. Point A (the center of gravity of the first block) is 1/2 from the right edge. Point B (the center of the two block system) is 1/4 away from the right edge of the second block. Let the starting point be the end of the second block (now we will move on to the third). For example, where is the center of gravity of single block #3? Half the length of this block, therefore, it is 1/2 + 1/4 = 3/4 from our reference point. Where is point C? In two thirds of the segment between 3/4 and 1/4, i.e. at the point before, we change the reference point to the right edge of the third block. The center of gravity of the three-block system is now removed from the new reference point, and so on. Center of gravity Cn a tower made up of n blocks is 1/2n away from the instantaneous reference point, which is the right edge of the base block, i.e. the nth block from the top.
Since the series of reciprocals diverges, we can get any large variation. Could this actually be implemented? It's like an endless brick tower - sooner or later it will collapse under its own weight. In our scheme, the minimal inaccuracies in block placement (and the slow increase in partial sums of the series) means we won't get very far.