Why don't we divide by zero?
Content
Readers may wonder why I devote an entire article to such a banal issue? The reason is the staggering number of students (!) casually carrying out the operation under the name. And not only students. Sometimes I catch and teachers. What will the students of such teachers be able to do in mathematics? The immediate reason for writing this text was a conversation with a teacher for whom division by zero was not a problem ...
With zero, yes, except for the hassle of nothing at all, because we do not really need to use it in everyday life. We don't go shopping for zero eggs. “There is one person in the room” sounds somehow natural, and “zero people” sounds artificial. Linguists say that zero is outside the language system.
We can do without the zero in bank accounts as well: just use - as on a thermometer - red and blue for positive and negative values (note that for temperature it is natural to use red for positive numbers, and for bank accounts it is the other way around, because the debit should trigger a warning, so red is highly recommended).
By including zero as a natural number, we touch on the problem of differentiation Cardinal numbers od household. Within 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …..
the power of the number is the same as the number of the place where it stands. Otherwise, it is already in the sequence 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …..
The number of singleton sets comes second, the number of sets with two elements comes third, and so on. We have to explain why, for example, we do not number the places of athletes in competitions from scratch. Then the first-place winner would receive a silver medal (gold went to the zero-place winner), and so on. A somewhat similar procedure was used in football - I don't know if Readers know that "league one" means "following the best." “, and the zero league is called to become the “major league”.
Sometimes we hear the argument that we need to start from scratch, because it is convenient for IT people. Continuing these considerations, the definition of a kilometer should be changed - it should be 1024 m, because this is the number of bytes in a kilobyte (I will refer to a joke known to computer scientists: “What is the difference between a freshman and a student of computer science and a fifth-year student of this faculty? that a kilobyte is 1000 kilobytes, the last - that a kilometer is 1024 meters")!
Another point of view, which should already be taken seriously, is this: we always measure from scratch! It is enough to look at any scale on the ruler, on household scales, even on the clock. Since we measure from zero, and counting can be understood as a measurement with a dimensionless unit, then we should count from zero.
It's a simple matter, but...
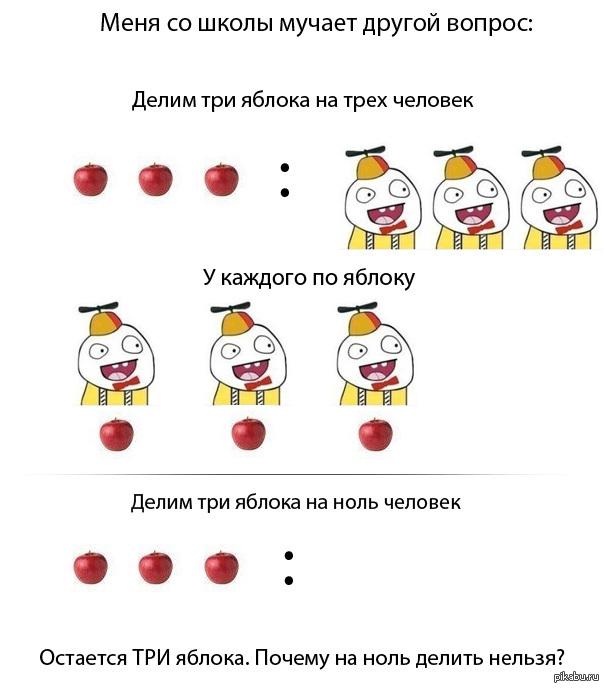
Let's leave the general reasoning and return to division by zero. The matter is simple and it would be simple if it were not for ... so what? Let's think and try. How much can it be - one divided by zero? Let's see: 1/0 = x. Multiply both sides by the denominator of the left side.
We get 1=0. Something is wrong! What happened? Ah guess! The assumption that there is a quotient of unity and zero leads to a contradiction. And if one cannot be divided by zero, then another number can. If, Reader, you shrug your shoulders and wonder why the author (that is, me) writes about such platitudes, then ... I am very glad!
The formula 0/0 = 0 could be defended on a stubborn basis, but it contradicts the rule that the result of dividing a number by itself is equal to one. Absolutely, but quite different are such symbols as 0/0, °/° and the like in calculus. They do not mean any number, but are symbolic designations for particular sequences of certain types.
In an electrical engineering book, I found an interesting comparison: dividing by zero is just as dangerous as high voltage electricity. This is normal: Ohm's law states that the ratio of voltage to resistance is equal to current: V = U / R. If resistance were zero, a theoretically infinite current would flow through the conductor, burning all possible conductors.
I once wrote a poem about the dangers of dividing by zero for every day of the week. I remember that the most dramatic day was Thursday, but it's a pity for all my work in this area.
When you divide something by zero
Very early Monday
Week what just happened
You've already failed miserably.
When Tuesday afternoon
You put zero in the denominator
I'll tell you then, you're wrong
Bad mathematician!
When through zero, through perversion,
Wanna split on Wednesday
You will get in a lot of trouble
You've got hay and water in your head!
A certain Bartek was with us.
He was at odds with the rules.
On Thursday, it is divisible by zero.
He is no longer between us!
If a strange desire takes hold of you
Divide by zero on Friday
I'll be honest, I'll be honest:
Bad start to this weekend.
When it's zero, somewhere on Saturday
The divider will be yours (not bold)
Kneel under the church fence.
This is your resurrection.
Do you want zero under the dash,
Make a holiday on Sunday
Bring chalk, black board.
Write: it is not divisible by zero!
Zero is associated with emptiness and nothingness. Indeed, he came to mathematics as a quantity that, when added to any, does not change it: x + 0 = x. But now zero appears in several other values, most notably as scale start. If outside the window there is neither positive temperature nor frost, then ... this is zero, which does not mean that there is no temperature at all. A zero-class monument is not one that has been demolished for a long time and simply does not exist. On the contrary, it is something like the Wawel, the Eiffel Tower and the Statue of Liberty.
Well, the importance of zero in a positional system can hardly be overestimated. Do you know, Reader, how many zeros does Bill Gates have in his bank account? I don't know, but I'd like half. Apparently, Napoleon Bonaparte noticed that people are like zeros: they acquire meaning through position. In Andrzej Wajda's film As the Years, As the Days Go by, the passionate artist Jerzy explodes: "The Philistine is zero, nihil, nothing, nothing, nihil, zero." But zero can be good: “zero deviation from the norm” means that everything is going well, and keep it up!
Let's get back to mathematics. Zero can be added, subtracted and multiplied with impunity. “I gained zero kilograms,” Manya says to Anya. “And this is interesting, because I lost the same weight,” Anya replies. So let's eat six zero servings of ice cream six times, it won't hurt us.
We cannot divide by zero, but we can divide by zero. A plate of zero dumplings can be easily handed out to those who are waiting for food. How much will each get?
Zero is not positive or negative. This and the number non-positiveи non-negative. It satisfies the inequalities x≥0 and x≤0. The contradiction "something positive" is not "something negative", but "something negative or equal to zero". Mathematicians, contrary to the rules of the language, will always say that something is "equal to zero" and not "zero." To justify this practice, we have: if we read the formula x = 0 "x is zero", then x = 1 we read "x is equal to one", which could be swallowed, but what about "x = 1534267"? You also cannot assign a numeric value to the character 00nor raise zero to a negative power. On the other hand, you can root zero at will... and the result will always be zero.
Exponential function y = ax, the positive base of a, never becomes zero. It follows that there is no zero logarithm. Indeed, the logarithm of a to base b is the exponent to which the base must be raised to obtain the logarithm of a. For a = 0, there is no such indicator, and zero cannot be the base of the logarithm. However, the zero in the "denominator" of Newton's symbol is something else. We assume that these conventions do not lead to a contradiction.
false evidence
Division by zero is a common subject for false proofs, and it happens even to experienced mathematicians. Let me give you two of my favorite examples. The first is algebraic. I will "prove" that all numbers are equal. Suppose there are two numbers that are not equal. Therefore, one of them is greater than the other, let a > b. Let us assume that c is their difference
c \uXNUMXd a - b. So we have a - b = c, whence a = b + c.
We multiply both parts of the latter by a - b:
a2 – ab = ab + ac – b2 – bc.
I translate ak to the left side, of course I remember about changing the sign:
a2 - ab - ac = ab - b2 - bc.
I exclude common factors:
A (a-b-c) \uXNUMXd b (a-b-c),
I share and I have what I wanted:
a = b.
And actually even stranger, because I assumed that a > b, and I got that a = b. If in the example above "cheating" is easy to recognize, then in the geometric proof below it is not so easy. I will prove that ... the trapezoid does not exist. The figure commonly called a trapezoid does not exist.
But suppose first that there is such a thing as a trapezoid (ABCD in the figure below). It has two parallel sides ("bases"). Let's stretch these bases, as shown in the picture, so that we get a parallelogram. Its diagonals divide the other diagonal of the trapezoid into segments whose lengths are denoted x, y, z, as in picture 1. From the similarity of the corresponding triangles, we obtain the proportions:
where we define:
Oraz
where we define:
Subtract the sides of equality marked with asterisks:
Shortening both sides by x − z, we get - a / b = 1, which means a + b = 0. But the numbers a, b are the lengths of the bases of the trapezoid. If their sum is zero, then they are also zero. This means that a figure like a trapezoid cannot exist! And since rectangles, rhombuses and squares are also trapezoids, then, dear Reader, there are no rhombuses, rectangles and squares either ...
Guess Guess
Sharing information is the most interesting and challenging of the four basic activities. Here, for the first time, we encounter a phenomenon so common in adulthood: "guess the answer, and then check if you guessed right." This is very aptly expressed by Daniel K. Dennett (“How to Make Mistakes?”, in How It Is – A Scientific Guide to the Universe, CiS, Warsaw, 1997):
This method of "guessing" does not interfere with our adult life - perhaps because we learn it early and guessing is not difficult. Ideologically, the same phenomenon occurs, for example, in mathematical (complete) induction. In the same place, we “guess” the formula and then check whether our guess is correct. Students always ask: “How did we know the pattern? How can it be taken out?" When students ask me this question, I turn their question into a joke: "I know this because I'm a professional, because I'm paid to know." Students at school can be answered in the same style, only more seriously.
An exercise. Note that we start addition and written multiplication with the lowest unit, and division with the highest unit.
A combination of two ideas
Math teachers have always pointed out that what we call adult separation is the union of two conceptually different ideas: Chassis i division.
The first one (Chassis) occurs in tasks where the archetype is:
Divide-divide These are tasks such as:
? (We retain the original style of this problem, taken from Julian Zgozalewicz's handbook published in Krakow in 1892 - the złoty is the Rhenish złoty, the currency that was in circulation in the Austro-Hungarian Empire until the beginning of the XNUMXth century).
Now consider two problems with the oldest mathematics textbook in Polish, father Tomasz Clos (1538). Is it a division or a coupe? Solve it the way schoolchildren in the XNUMXth century should:
(Polish to Polish translation: There is a quart and four pots in a barrel. A pot is four quarts. Someone bought 20 barrels of wine for 50 zł for trade. Duty and tax (excise?) will be 8 zł. How much to sell a quart to earn 8 zł?)
Sports, physics, congruence
Sometimes in sports you have to divide something by zero (goal ratio). Well, the judges somehow deal with it. However, in abstract algebra they are on the agenda. non-zero quantitieswhose square is zero. It can even be explained simply.
Consider a function F that associates a point (y, 0) with a point in the plane (x, y). What is F2, that is, a double execution of F? Zero function - each point has an image (0,0).
Finally, non-zero quantities whose square is 0 are almost daily bread for physicists, and numbers of the form a + bε, where ε ≠ 0, but ε2 = 0, mathematicians call double numbers. They occur in mathematical analysis and in differential geometry.
After all, there is something in arithmetic that has division by zero in at least the name. It comes from congruence. Let Z denote the set of integers. Dividing the set Z by p means that we equate each number (integer) to some others, namely, to those by which their difference is divisible. So, when we have five types of numbers corresponding to the numbers 0, 1, 2, 3, 4 - the possible remainders when divided by 5. The formula is written like this:
mod when the difference is a multiple.
For = 2, we have only two numbers: 0 and 1. Dividing integers into two such classes is equivalent to dividing them into even and odd. Let's replace it now. The difference is always divisible by 1 (any integer is divisible by 1). Is it possible to take =0? Let's try: when is the difference of two numbers a multiple of zero? Only when these two numbers are equal. So dividing a set of integers by zero makes sense, but it's not interesting: nothing happens. However, it should be emphasized that this is not division of numbers in the sense known from elementary school.
Such actions are simply forbidden, as well as long and wide mathematics.
Rice. 2. Identification of numbers using comparison
(mode 5 and mode 2)

