Journey into the unreal world of mathematics

I wrote this article in one of the environments, after a lecture and practice in a college of computer science. I defend myself against criticism of the students of this school, their knowledge, attitude to science and, most importantly, their teaching skills. This... nobody teaches them.

Why am I so defensive? For a simple reason - I am at an age when, probably, the world around us is not yet understood. Maybe I'm teaching them to harness and unharness horses, and not to drive a car? Maybe I teach them to write with a quill pen? Although I have a better opinion of a person, I consider myself “following”, but…

Until recently, in high school, they talked about complex numbers. And it was on this Wednesday that I came home, quit - almost none of the students have yet learned what it is and how to use these numbers. Some look at all mathematics like a goose at a painted door. But I was also genuinely surprised when they told me how to learn. Simply put, each hour of a lecture is two hours of homework: reading a textbook, learning how to solve problems on a given topic, etc. Having prepared in this way, we come to the exercises, where we improve everything ... Pleasantly, the students, apparently, thought that sitting at the lecture - most often looking out the window - already guarantees the entry of knowledge into the head.

Stop! Enough of this. I will describe my answer to a question that I received during a class with fellows from the National Children's Fund, an institution that supports talented children from all over the country. The question (or rather the suggestion) was:

— Could you tell us something about unreal numbers?

“Of course,” I replied. 

The reality of numbers

“A friend is another me, friendship is the ratio of numbers 220 and 284,” said Pythagoras. The point here is that the sum of the divisors of the number 220 is 284, and the sum of the divisors of the number 284 is 220:

1 + 2 + 4 + 71 + 142 = 220

1 + 2 + 4 + 5 + 10 = 11 + 20 + 22 + 44 + 55 + 110 = 284

Another interesting coincidence between the numbers 220 and 284 is this: the seventeen highest prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53 , and 59.

Their sum is 2x220, and the sum of the squares is 59x284.

First. There is no concept of "real number". It's like after reading an article about elephants, you ask, "Now we're going to ask for non-elephants." There are whole and non-whole, rational and irrational, but there are no unreal. Specifically: numbers that are not real are not called invalid. There are many types of "numbers" in mathematics, and they differ from each other, like - to take a zoological comparison - an elephant and an earthworm.

Secondly, we will perform operations that you may already know are forbidden: extracting the square roots of negative numbers. Well, mathematics will overcome such barriers. Does it make sense though? In mathematics, as in any other science, whether a theory enters forever into the repository of knowledge depends ... on its application. If it is useless, then it ends up in the trash, then in some rubbish of the history of knowledge. Without the numbers that I talk about at the end of this article, it is impossible to develop mathematics. But let's start with some small things. What are real numbers, you know. They fill the number line densely and without gaps. You also know what natural numbers are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …….. - all of them will not fit in memory even the greatest. They also have a beautiful name: natural. They have so many interesting properties. How do you like this:

1 + 15 + 42 + 98 + 123 + 179 + 206 + 220 = 3 + 11 + 46 + 92 + 129 + 175 + 210 + 218

1² + 15² + 42² + 98² + 123² + 179² + 206² + 220² = 3² + 11² + 46² + 92² + 129² + 175² + 210² + 218²

1³ + 15³ + 42³ + 98³ + 123³ + 179³ + 206³ + 220³ = 3³ + 11³ + 46³ + 92³ + 129³ + 175³ + 210³ + 218³

1⁴ + 15⁴ + 42⁴ + 98⁴ + 123⁴ + 179⁴ + 206⁴ + 220⁴ = 3⁴ + 11⁴ + 46⁴ + 92⁴ + 129⁴ + 175⁴ + 210⁴ + 218⁴

1⁵ + 15⁵ + 42⁵ + 98⁵ + 123⁵ + 179⁵ + 206⁵ + 220⁵ = 3⁵ + 11⁵ + 46⁵ + 92⁵ + 129⁵ + 175⁵ + 210⁵ + 218⁵

1⁶ + 15⁶ + 42⁶ + 98³ + 123⁶ + 179⁶ + 206⁶ + 220⁶ = 3⁶ + 11⁶ + 46⁶ + 92⁶ + 129⁶ + 175⁶ + 210⁶ + 218⁶

1⁷ + 15⁷ + 42⁷ + 98³ + 123⁷ + 179⁷ + 206⁷ + 220⁷ = 3⁷ + 11⁷ + 46⁷ + 92⁷ + 129⁷ + 175⁷ + 210⁷ + 218⁷

“It is natural to be interested in the natural numbers,” said Karl Lindenholm, and Leopold Kronecker (1823–1891) put it succinctly: “God created the natural numbers—everything else is the work of man!” Fractions (called rational numbers by mathematicians) also have amazing properties:

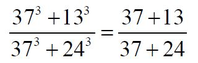
and in equality:

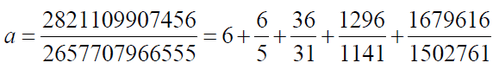
you can, starting from the left side, rub the pluses and replace them with multiplication signs - and the equality will remain true:

And so on.

As you know, for fractions a/b, where a and b are integers, and b ≠ 0, they say rational number. But only in Polish they call themselves that. They speak English, French, German and Russian. rational number. In English: rational numbers. Irrational numbers it's irrational, irrational. We also speak Polish about irrational theories, ideas and deeds - this is madness, imaginary, inexplicable. They say that women are afraid of mice - isn't that so irrational?

In ancient times, numbers had a soul. Each meant something, each symbolized something, each reflected a particle of that harmony of the Universe, that is, in Greek, the Cosmos. The very word "cosmos" means exactly "order, order". The most important were six (the perfect number) and ten, the sum of the consecutive numbers 1+2+3+4, made up of other numbers, the symbolism of which has survived to this day. So Pythagoras taught that numbers are the beginning and source of everything, and only the discovery irrational numbers turned the Pythagorean movement towards geometry. We know the reasoning from school that

√2 is an irrational number

For suppose that there is: and that this fraction cannot be reduced. In particular, both p and q are odd. Let's square: 2q²=p². The number p cannot be odd, since then p² would also be, and the left side of the equality is a multiple of 2. Hence, p is even, i.e., p = 2r, hence p²= 4r². We reduce the equation 2q²= 4r² by 2. We get q²= 2r² and we see that q must also be even, which we assumed is not so. The resulting contradiction completes the proof - this formula can often be found in every mathematical book. This circumstantial proof is a favorite trick of the sophists.

This immensity could not be understood by the Pythagoreans. Everything must be able to be described by numbers, and the diagonal of a square, which anyone can draw with a stick across the sand, has no, that is, measurable, length. “Our faith was in vain,” the Pythagoreans seem to say. How so? It's kind of... irrational. The Union tried to save itself by sectarian methods. Anyone who dares to reveal their existence irrational numbers, was to be punished by death, and, apparently, the first sentence was carried out by the master himself.

But "the thought passed unscathed." The golden age has arrived. The Greeks defeated the Persians (Marathon 490, Block 479). Democracy was strengthened, new centers of philosophical thought and new schools arose. The Pythagoreans were still struggling with irrational numbers. Some preached: we will not comprehend this mystery; we can only contemplate and marvel at Uncharted. The latter were more pragmatic and did not respect the Mystery. At that time, two mental constructions appeared that made it possible to understand irrational numbers. The fact that we understand them well enough today belongs to Eudoxus (XNUMXth century BC), and it was only at the end of the XNUMXth century that the German mathematician Richard Dedekind gave the theory of Eudoxus the proper development in accordance with the requirements of rigorous mathematical logic.

Mass of figures or torture

Could you live without numbers? Even if what life would be... We would have to go to the store to buy shoes with a stick, which we previously measured the length of the foot. “I would like apples, ah, here it is!” – we would show sellers in the market. "How far is it from Modlin to Nowy Dwur Mazowiecki"? “Pretty close!”

Numbers are used to measure. With their help, we also express many other concepts. For example, the scale of the map shows how much the area of ​​the country has decreased. A two-to-one scale, or simply 2, expresses the fact that something has been doubled in size. Let's say mathematically: each homogeneity corresponds to a number - its scale.

The task. We made a xerographic copy, magnifying the image several times. Then the enlarged fragment was again enlarged b times. What is the general magnification scale? Answer: a × b multiplied by b. These scales need to be multiplied. The "minus one" number, -1, corresponds to one precision that is centered, i.e. rotated 180 degrees. What number corresponds to a 90 degree turn? There is no such number. It is, it is… or rather, it will be soon. Are you ready for moral torture? Take courage and take the square root of minus one. I'm listening to? What can't you? After all, I told you to be brave. Pull it out! Hey, well, pull, pull... I'll help... Here: -1 Now that we have it, let's try to use it... Of course, now we can extract the roots of all negative numbers, for example .:

√-4 = 2√-1,-16 = 4√-1

“Regardless of the mental anguish it entails.” This is what Girolamo Cardano wrote in 1539, trying to overcome the mental difficulties associated with - as it soon came to be called - imaginary quantities. He considered these...

...The task. Divide 10 into two parts, the product of which is 40. I remember that from the previous episode he wrote something like this: Certainly impossible. However, let's do this: divide 10 into two equal parts, each equal to 5. Multiply them - it turned out 25. From the resulting 25, now subtract 40, if you like, and you get -15. Now look: √-15 added and subtracted from 5 gives you the product of 40. These are the numbers 5-√-15 and 5 + √-15. The verification of the result was carried out by Cardano as follows:

“Regardless of the heartache it entails, multiply 5 + √-15 by 5-√-15. We get 25 - (-15), which is equal to 25 + 15. So, the product is 40 .... It's really difficult."

Well, how much is: (1 + √-1) (1-√-1)? Let's multiply. Remember that √-1 × √-1 = -1. Great. Now a more difficult task: from a + b√-1 to ab√-1. What happened? Certainly, like this: (a + b√-1) (ab√-1) = a²+b²

What's interesting about this? For example, the fact that we can factorize expressions that we "did not know before." The abbreviated multiplication formula for²-b² Do you remember the formula for²+b² it wasn't, because it couldn't be. In the domain of real numbers, the polynomial²+b² it is unavoidable. Let's denote "our" square root of "minus one" with the letter i.²= -1. It's an "unreal" prime number. And that's what describes a 90 degree turn of an airplane. Why? After all,²= -1, and combining one 90-degree rotation and another 180-degree rotation gives a 45-degree rotation. What type of rotation is being described? Obviously a XNUMX degree turn. What does the -i mean? It's a little more complicated:

(-I)² = -i × (-i) = + i² =-1

So -i also describes a 90 degree rotation, just in the opposite direction of i's rotation. Which one is left and which one is right? You must make an appointment. We assume that the number i specifies a rotation in a direction that mathematicians consider positive: counterclockwise. The number -i describes rotation in the direction the pointers are moving.

But do numbers like i and -i exist? Are! We just brought them to life. I'm listening to? That they exist only in our head? Well what to expect? All other numbers also exist only in our mind. We need to see if our newborn numbers survive. More precisely, whether the design is logical and whether they will be useful for something. Please take my word for it that everything is in order and that these new numbers are really helpful. Numbers like 3+i, 5-7i, more generally: a+bi are called complex numbers. I showed you how you can get them by spinning the plane. They can be entered in different ways: as points in a plane, as some polynomials, as some kind of numerical arrays ... and each time they are the same: the equation x² +1=0 there is no element... hocus pocus is already there!!!! Let's rejoice and rejoice!!!

End of tour

This concludes our first tour of the country of fake numbers. Of the other unearthly numbers, I will also mention those that have an infinite number of digits in front, and not behind (they are called 10-adic, for us p-adic are more important, where p is a prime number), for example X = … … … 96109004106619977392256259918212890625

Let's count X please². Because? What if we calculate the square of a number followed by an infinite number of digits? Well, let's do the same. We know that x² = X.

Let's find another such number with an infinite number of digits in front that satisfies the equation. Hint: the square of a number that ends in six also ends in six. The square of a number that ends in 76 also ends in 76. The square of a number that ends in 376 also ends in 376. The square of a number that ends in 9376 also ends in 9376. The square of a number that ends in XNUMX on … There are also numbers that are so small that, being positive, they remain smaller than any other positive number. They are so tiny that sometimes it is enough to square them to get zero. There are numbers that do not satisfy the condition a × b = b × a. There are also infinite numbers. How many natural numbers are there? Infinitely many? Yes, but how much? How can this be expressed as a number? Answer: the smallest of infinite numbers; it is marked with a beautiful letter: A and supplemented with a zero index A₀ , aleph-zero.

There are also numbers that we don't know exist... or that you can believe or disbelieve as you please. And speaking of the like: I hope you still like Unreal Numbers, Fantasy Species Numbers.